数据分析：描述性统计（基础、案例、代码）

? 描述性统计：从总体数据中提取出变量的主要信息（比如均值、总和等），从而从总体层面上描述数据的特征！

? 统计量：提取的统计信息 —— 就是统计量

1、统计量包括：常用10个

• 频数 与 频率：频数、频率
• 集中趋势分析：均值、中位数、众数、分位数
• 离散程度分析：极差、方差、标准差
• 分布形状：偏度、峰度

2、变量的类型

? 类别变量：无序类别（名义变量）、有序类别（等级变量）

• 比如颜色，有红、黄、蓝… 每个都是一个类别 —— 且是无序类别，没有谁大于谁一说
• 比如职位，有总经理、经理、普通员工…每个也是一个类别 —— 且是有序类别，通常总经理 > 经理 > 普通员工

? 数值变量：连续变量、离散变量

• 连续：取尽区间中 每一个取值 —— 比如1小时到2小时候之间有多少个数值呢？无数多个
• 离散：不能取尽区间中的每一个取值，通常是整数 —— 比如公司人数，不可能出现100.5个吧，人数都是整数

频数 与 频率

数据的频数 与 频率统计 适用于 类别变量

• 频数：数据中类别变量 每个不同的值 出现的次数（具体数量）
• 频率：每个类别变量 与 总次数的 比值（百分比）

集中趋势

• 均值：平均值（总和/个数）
• 中位数：数据先 升序排列，位于最中间的那个值即 中位数。（如果中间有2个，再接着取这2个数的均值） —— 总之中位数只有一个
• 众数：数据中出现次数最多的那个值

? 注意

1. 数值变量通常使用 均值 中值 表示集中趋势
2. 类别变量通常使用 众数 表示集中趋势
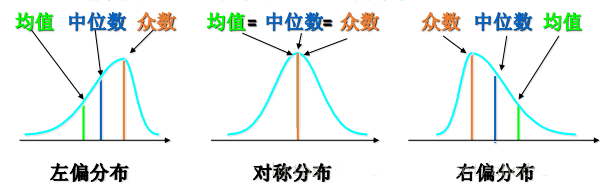
3. 在 正态分布 下，3者一样。偏态分布下，3者不同
4. 均值 容易受到 极端值 影响
5. 中值 众数 不受极端值影响，更稳定
6. 众数 可能不唯一

? 注意

左偏和右偏怎么区分？看哪边少就是往哪边便~

收入 ——> 典型右偏分布，严重右偏，少量的极大值（马云）…

收入 ——> 要用中位数衡量(连续变量)

为什么不能用众数？收入并不是离散型变量~

分位数

通过n-1个 分位 将数据划分为 n 个区间，使得每个区间 数值的个数 相等（或近似相等）

n为分位数的 数量，常用的有 4分位 与 百分位

四分位

• 第1个分位 1/4 分位（下四分位）—— 数据中有 1/4 的数值 小于 该分位值
• 第2个分位 2/4 分位（中四分位）—— 数据中有 2/4 的数值 小于 该分位值（中位数）
• 第3个分位 3/4 分位（上四分位）—— 数据中有 3/4 的数值 小于 该分位值

四分位计算原理

? 注意：四分位的值不一定等于数据中的 某个值

步骤1：计算四分位的 位置

• Q1_index = （n-1）* 0.25
• Q2_index = （n-1）* 0.5
• Q3_index = （n-1）* 0.75
• ps：这里的n为数组中元素的 个数

步骤2：根据位置计算四分位的 值

• 当index为整数，四分位的值就是根据索引index取得的值
• 当index不为整数，四分位的值介于ceil(index) 与 floor(index) 之间（注意不是左右两个数的均值哦~），根据这两个位置的元素确定四分位值，根据权重计算具体的分位值

Numpy\Pandas中计算分位值

# numpy
import numpy as np

x = np.arange(10, 20)
# 自定义分位
print(np.quantile(x, q=[0.25, 0.5, 0.75]))
print(np.percentile(x, q=[25, 50, 75]))

# pandas 
x = [1, 3, 10, 15, 18, 20, 23, 40]
x_sel = pd.Series(x)
print(x_sel.describe())
print()
print('1/4分位的值:', x_sel.describe().loc['25%'])
# 自定义分位
print()
print(x_sel.describe(percentiles=[0.3, 0.9]))

离散程度

• 极差：最大值 – 最小值 —— 实际应用中基本不用极差
• 方差：体现一组数据中，每个值 与 均值 偏离的大小
• 标准差：方差的开方

? 注意：

1. 极差计算简单，但没有充分利用到数据信息
2. 方差、标准差可以提现数据的分散性，方差、标准差越大，数据越分散，相反则越居中
3. 方差、标准差还可以提现数据的波动性（稳定性），越大波动越大，相反则波动越小

# 以鸢尾花花萼长度为例， 计算极差，方差，标准差

# 1. 极差
sub = sepal_length.max() - sepal_length.min()
sub = np.ptp(sepal_length)
# 2. 方差
var = sepal_length.var()
# 3. 标准差
std = sepal_length.std()
print(sub, var, std)

分布形状

? 标准正态分布 —— 均值为0，标准差为1，np.random.normal(0, 1, size=10000)

偏度：统计数据分布 偏斜方向 和 程度 的度量（统计数据非对称程度的数字特征）

• 偏度为0 —— 正态分布
• 偏度<0 —— 左偏分布
• 偏度>0 —— 右偏分布

峰度：描述总体数据中数据分布的高矮程度。比较的对象是标准正态分布

常用来检验数据是否符合正态分布

• 峰度=0 —— 标准正态分布
• 峰度<0 —— 密度图 低于 标准正态分布（矮）—— 数据更分散，各个数据距离均值远，方差、标准差大
• 峰度>0 —— 密度图 高于 标准正态分布（高）—— 数据更密集，各个数据距离均值近，方差、标准差小